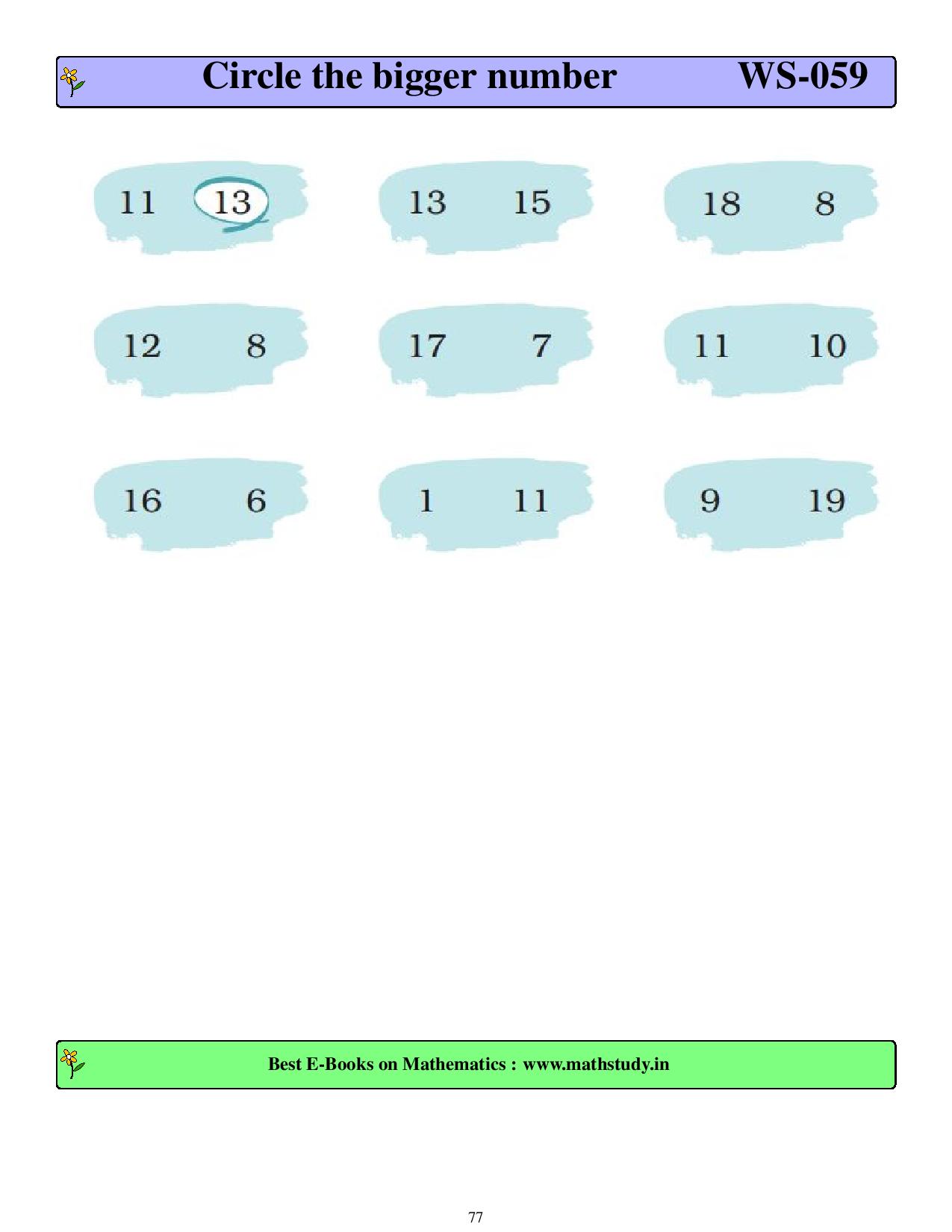
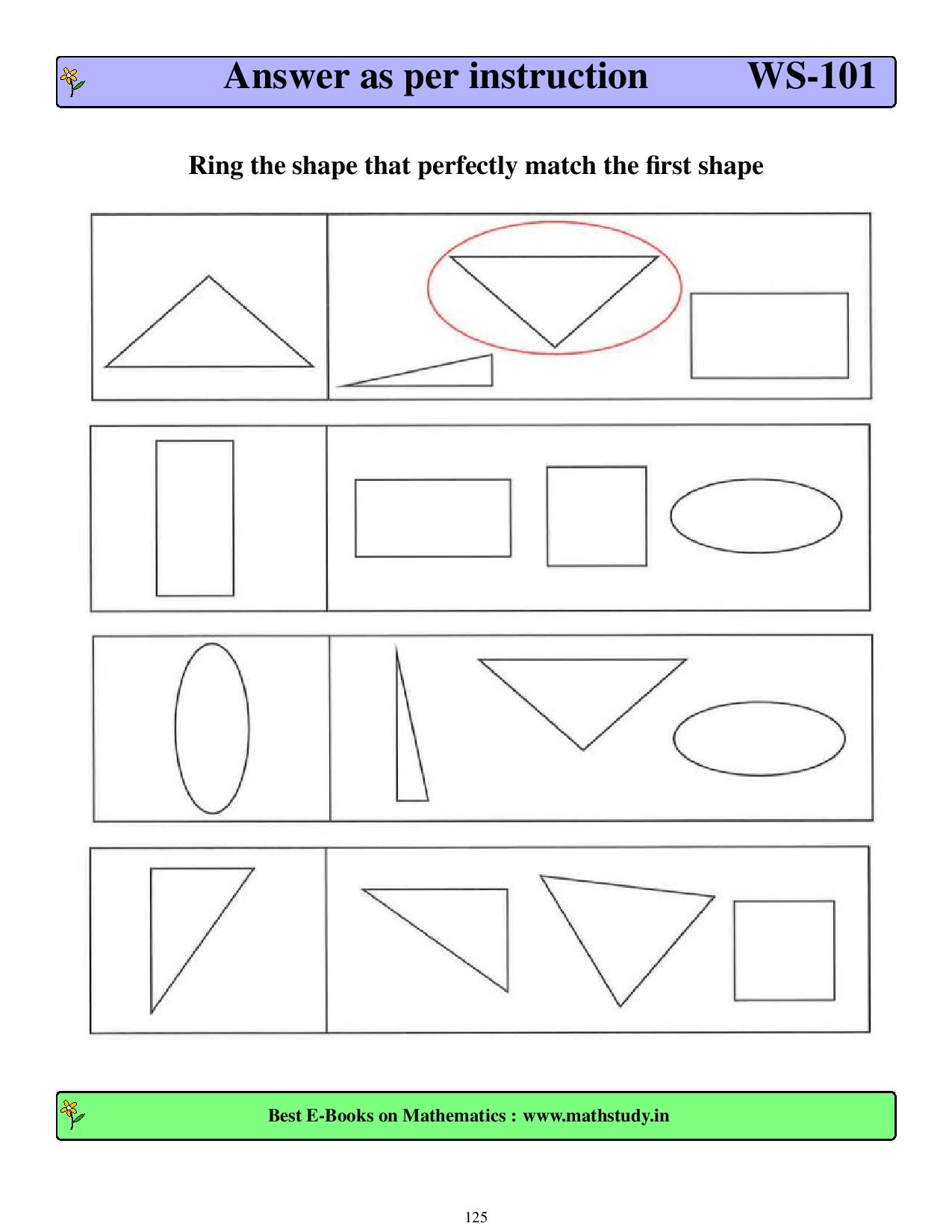
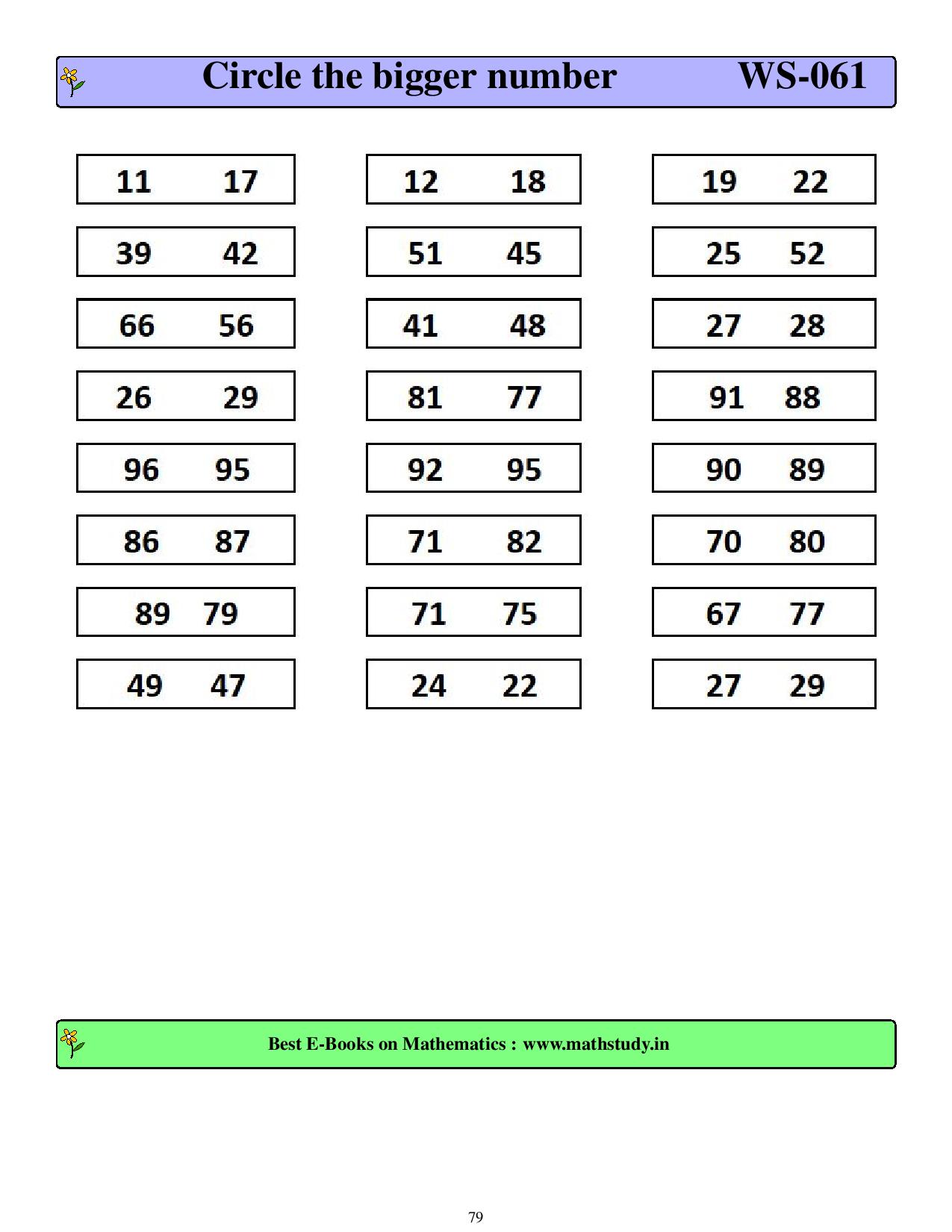
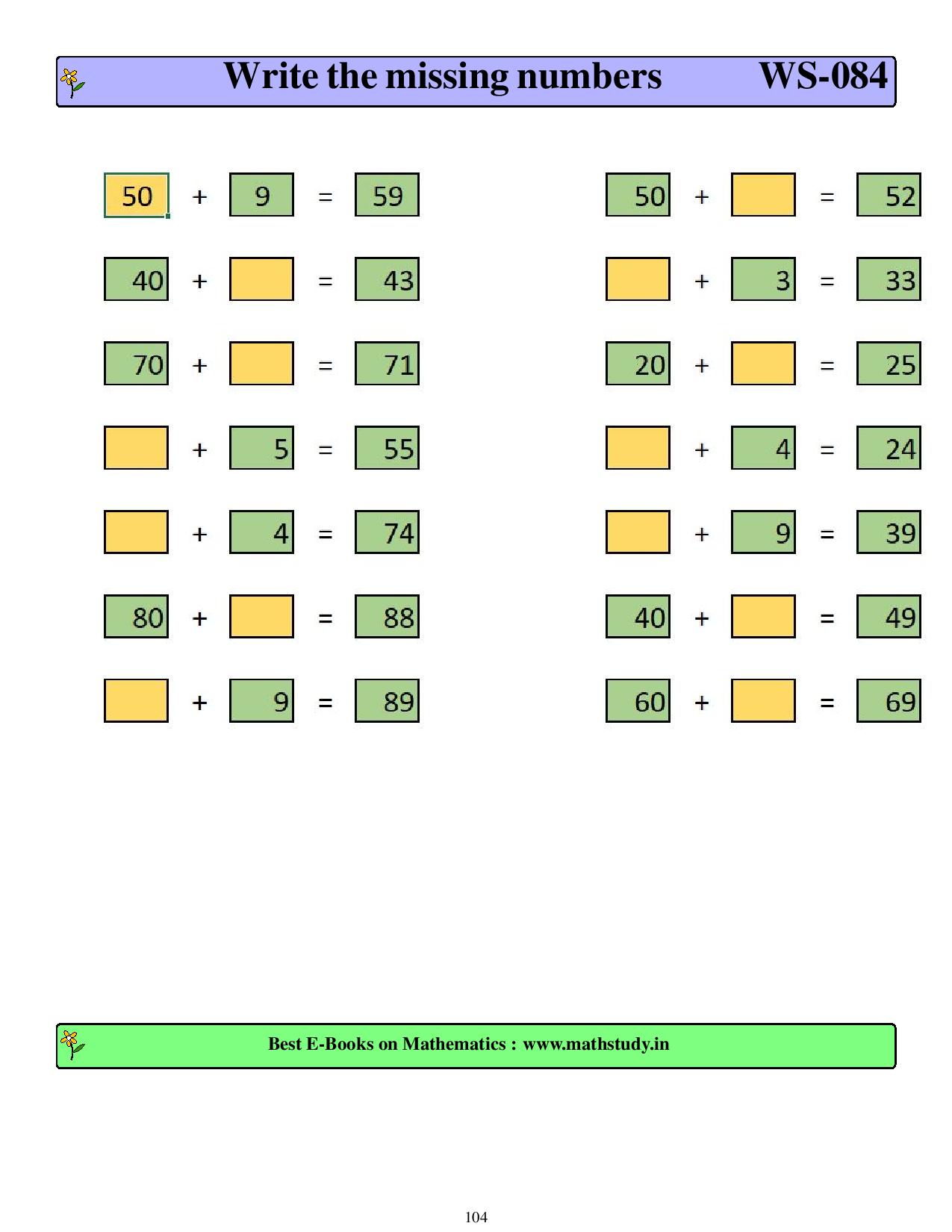
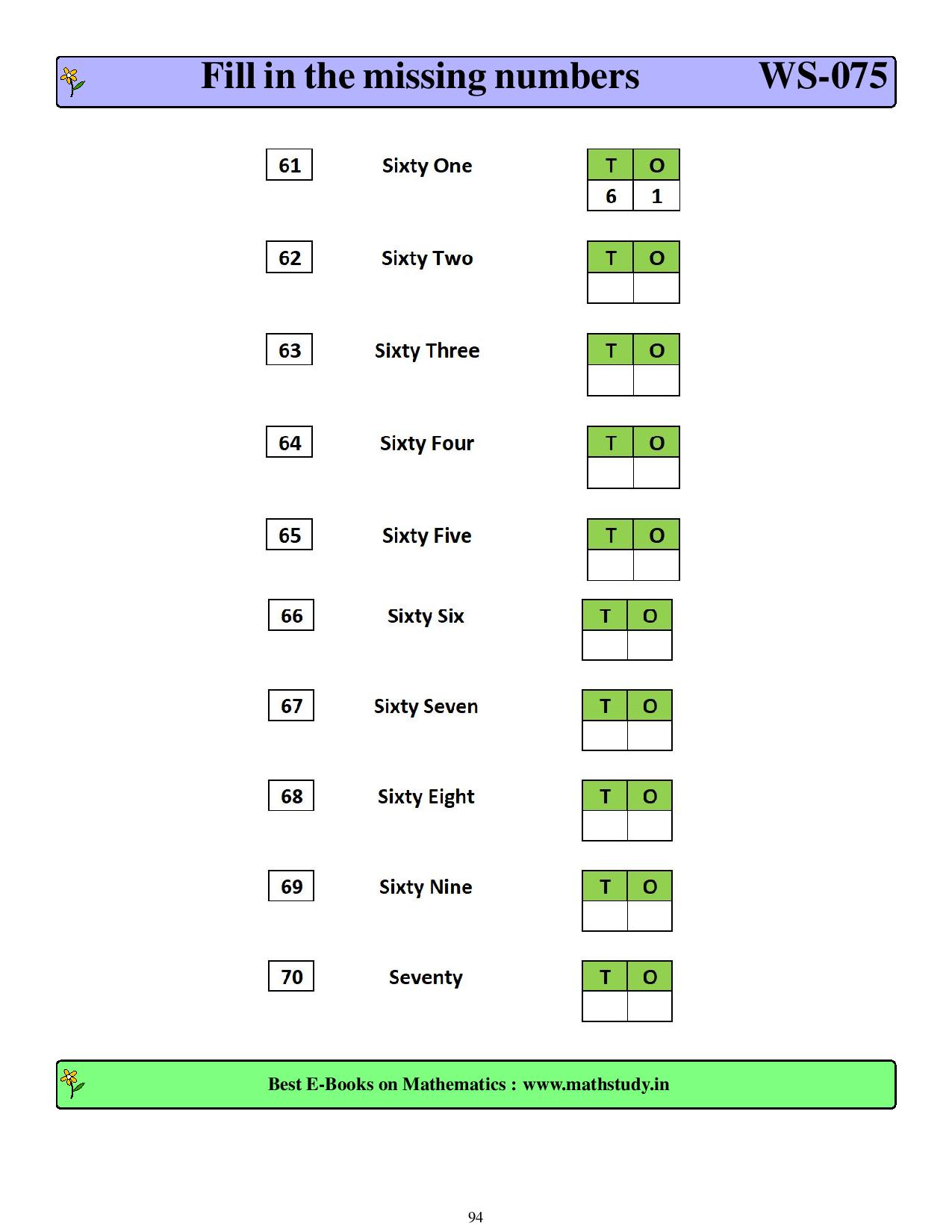
first grade worksheets-free printable worksheets More than 150 worksheets. Worksheets on word problems which are fully solved HOTS(Higher Order Thinking Skills) questions are included to enhance the level of understanding. Help students to score in mathematics competition like International Mathematics Olympiad. Help student to develop analytical mind frame. Highly useful for those who want to learn programming language and conding. As per the international standard of curriculum and can be used by any student across the globe. Highly useful for parents,schools,teachers and coaching institutes.
1st grade math worksheets pdf
1st grade math worksheets pdf More than 150 worksheets. Worksheets on word problems which are fully solved HOTS(Higher Order Thinking Skills) questions are included to enhance the level of understanding. Help students to score in mathematics competition like International Mathematics Olympiad. Help student to develop analytical mind frame. Highly useful for those who want to learn programming language and conding. As per the international standard of curriculum and can be used by any student across the globe. Highly useful for parents,schools,teachers and coaching institutes.
mental maths worksheets grade 1
mental maths worksheets grade 1 More than 150 worksheets. Worksheets on word problems which are fully solved HOTS(Higher Order Thinking Skills) questions are included to enhance the level of understanding. Help students to score in mathematics competition like International Mathematics Olympiad. Help student to develop analytical mind frame. Highly useful for those who want to learn programming language and conding. As per the international standard of curriculum and can be used by any student across the globe. Highly useful for parents,schools,teachers and coaching institutes.
1st grade math worksheets printable
1st grade math worksheets printable More than 150 worksheets. Worksheets on word problems which are fully solved HOTS(Higher Order Thinking Skills) questions are included to enhance the level of understanding. Help students to score in mathematics competition like International Mathematics Olympiad. Help student to develop analytical mind frame. Highly useful for those who want to learn programming language and conding. As per the international standard of curriculum and can be used by any student across the globe. Highly useful for parents,schools,teachers and coaching institutes.
free grade 1 math worksheets pdf download
free grade 1 math worksheets pdf download More than 150 worksheets. Worksheets on word problems which are fully solved HOTS(Higher Order Thinking Skills) questions are included to enhance the level of understanding. Help students to score in mathematics competition like International Mathematics Olympiad. Help student to develop analytical mind frame. Highly useful for those who want to learn programming language and conding. As per the international standard of curriculum and can be used by any student across the globe. Highly useful for parents,schools,teachers and coaching institutes.
cbse and ncert worksheets for class 1
cbse and ncert worksheets for class 1 More than 150 worksheets. Worksheets on word problems which are fully solved HOTS(Higher Order Thinking Skills) questions are included to enhance the level of understanding. Help students to score in mathematics competition like International Mathematics Olympiad. Help student to develop analytical mind frame. Highly useful for those who want to learn programming language and conding. As per the international standard of curriculum and can be used by any student across the globe. Highly useful for parents,schools,teachers and coaching institutes.
maths class 1 online classes
maths class 1 online classes More than 150 worksheets. Worksheets on word problems which are fully solved HOTS(Higher Order Thinking Skills) questions are included to enhance the level of understanding. Help students to score in mathematics competition like International Mathematics Olympiad. Help student to develop analytical mind frame. Highly useful for those who want to learn programming language and conding. As per the international standard of curriculum and can be used by any student across the globe. Highly useful for parents,schools,teachers and coaching institutes.
maths online practice tests quizzes for grade 1
maths online practice tests quizzes for grade 1 More than 150 worksheets. Worksheets on word problems which are fully solved HOTS(Higher Order Thinking Skills) questions are included to enhance the level of understanding. Help students to score in mathematics competition like International Mathematics Olympiad. Help student to develop analytical mind frame. Highly useful for those who want to learn programming language and conding. As per the international standard of curriculum and can be used by any student across the globe. Highly useful for parents,schools,teachers and coaching institutes.
grade 1 maths homework
grade 1 maths homework More than 150 worksheets. Worksheets on word problems which are fully solved HOTS(Higher Order Thinking Skills) questions are included to enhance the level of understanding. Help students to score in mathematics competition like International Mathematics Olympiad. Help student to develop analytical mind frame. Highly useful for those who want to learn programming language and conding. As per the international standard of curriculum and can be used by any student across the globe. Highly useful for parents,schools,teachers and coaching institutes.
engaging math worksheets for class 1
engaging math worksheets for class 1 More than 150 worksheets. Worksheets on word problems which are fully solved HOTS(Higher Order Thinking Skills) questions are included to enhance the level of understanding. Help students to score in mathematics competition like International Mathematics Olympiad. Help student to develop analytical mind frame. Highly useful for those who want to learn programming language and conding. As per the international standard of curriculum and can be used by any student across the globe. Highly useful for parents,schools,teachers and coaching institutes.